UJI BEDA RATA-RATA
.
KONSEP
DAN PRINSIP DASAR UJI BEDA RATA-RATA
Prinsip uji beda rata-rata dua
populasi independen adalah bahwa kedua populasi tidak memiliki hubungan (saling
independen). Artinya populasi satu tidak bergantung kepada populasi yang lain.
Misalnya kita ingin tahu apakah ada perbedaan rata-rata nilai mata kuliah
Statistik antara mahasiwa Fak. Kedokteran yang diberikan tutorial dengan
mahasiswa Fak. Kedokteran yang tidak diberikan tutorial.
Pengujian Perbedaan Rata‐rata Dua sampel saling bebas (Independent two sample ) Penelitian eksperimen biasanya menggunakan dua sampel atau lebih sebagai objek penelitiannya. Sampel-sampel tersebut dibandingkan untuk melihat ada-tidaknya perbedaan setelah sampel-sampel tersebut diberi perlakuan berbeda. Untuk melihat ada-tidaknya perbedaan, dilakukan uji perbedaan dua rata-rata.
Uji hipotesis dua rata-rata digunakan untuk mengetahui ada atau tidak adanya perbedaan (kesamaan) rata antara dua buah data. Salah satu teknik analisis statistik untuk menguji hipotesis dua rata-rata. Pengujian ini merupakanuji statistik parametrik yang tentu saja harrus memenuhi asumsi:
Uji hipotesis dua rata-rata digunakan untuk mengetahui ada atau tidak adanya perbedaan (kesamaan) rata antara dua buah data. Salah satu teknik analisis statistik untuk menguji hipotesis dua rata-rata. Pengujian ini merupakanuji statistik parametrik yang tentu saja harrus memenuhi asumsi:
- Data berdistribusi normal
- Data diplih secara acak
- Data yang digunakan merupakan dat numerik (skala & interval)
Pertanyaanya bagaimana jika asumsi diatas tidak bisa terpenuhi? maka caranya yaitu mengganti metode dari parametrik menjadi non-parametrik. untuk metode ini belum dijelaskan atau belum dibuat. segeara akan dibuatkan untuk metode ini.
Hipotesis yang digunakan dalam Pengujian Perbedaan Rata‐rata Dua sampel saling bebas ada 3 hampir sama dengan yang lainnya yaitu:
1. Hipotesis dua arah yaitu rata-rata antar kelompok sama
2. Hipotesis satu arah menganggap kelompok 1 lebih tinggi rata-ratanya dibandingkan kelompok
3. Hipotesis satu arah yang menganggap kelompok 1 lebih kecil rata-ratanya dibandingkan kelompok
Dalam Pengujian Perbedaan Rata‐rata Dua sampel saling bebas (Independent two sample ) ada 4 jenis mencari statistik uji dari Pengujian Perbedaan Rata‐rata Dua sampel saling bebas (Independent two sample):
Hipotesis yang digunakan dalam Pengujian Perbedaan Rata‐rata Dua sampel saling bebas ada 3 hampir sama dengan yang lainnya yaitu:
1. Hipotesis dua arah yaitu rata-rata antar kelompok sama
2. Hipotesis satu arah menganggap kelompok 1 lebih tinggi rata-ratanya dibandingkan kelompok
3. Hipotesis satu arah yang menganggap kelompok 1 lebih kecil rata-ratanya dibandingkan kelompok
Dalam Pengujian Perbedaan Rata‐rata Dua sampel saling bebas (Independent two sample ) ada 4 jenis mencari statistik uji dari Pengujian Perbedaan Rata‐rata Dua sampel saling bebas (Independent two sample):
Varians populasi diketahui: Cara ini dapat digunakan apabila kita mengetahui nilai varians populasi itu sendiri.sehingga cara ini mungkin jarang digunakan karena untuk mengetahui nilai populasi. berikut cara mencari z-hitung:
apabila kita tidak mengetahui nilai populasi khususnya simpangan baku maka kita bisa menggunakan uji-t. dalam uji t ini dibagi menjadi tiga bagian.
Varians populasi tidak diketahui, ukuran sampel sama dan Varians diasumsikan sama
Varians populasi tidak diketahui, ukuran sampel sama dan Varians diasumsikan sama
Cara ini dapat digunakan jika ukuran sampel (n) sama dan juga varians homogen/sama. ini kadang diasumsikan untuk memecahkan masalah penelitian. berikut uji t yang digunakan:
dimana,
Sx1x2 disebut juga pool standar deviasi yang merupakan penggabungan dua standar deviasi. pada t-hitung ini menggunakandegree of freedom dengan rumus 2n-2.
Varians populasi tidak diketahui, Ukuran sampel berbeda dan varians diasumsikan sama.Walaupun varians homogen tapi ukuran sampel yang digunakan berbeda maka rumus di atas tidak dapat digunakan. sehingga perlu menggunakan t-hitung yang baru sebagai berikut:
dimana,
selain itu degree of freedom pun berubah. degree of freedom untuk kasus ini yaitu n1+n2-2
Varians populasi tidak diketahui, Ukuran sampel sama/berbeda, Varians diasumsikan berbeda.Tes ini juga disebut denganwelch's test dan hanya digunakan apabila varians diasumsikan berbeda (baik ukuran sampel sama atau berbeda). berikut cara menghitung t statistik:
Varians populasi tidak diketahui, Ukuran sampel sama/berbeda, Varians diasumsikan berbeda.Tes ini juga disebut denganwelch's test dan hanya digunakan apabila varians diasumsikan berbeda (baik ukuran sampel sama atau berbeda). berikut cara menghitung t statistik:
dimana,
persamaan ini juga dikenal denganPersamaan welch satterthwaite
Langkah-Langkah Uji Kesamaan Dua Rata-Rata (Usman & Akbar, 2009)
1) Uji atau asumsikan bahwa data dipilih secara acak
2) Uji atau asumsikan bahwa data berdistribusi normal
3) tentukan apakah variansnya homogen atau hetero?
4) Tulis Ha dan H0 dalam bentuk kalimat
5) Tulis Ha dan H0 dalam bentuk statistik
6) Cari t-hitung atau z-hitung dengan rumus tertentu
7) Tentukan taraf signifikan (α)
8) Cari t-tabel atau z-tabel dengan pengujian dua pihak dimana df yang tergantung rumus.
9) Tentukan kriteria pengujian, yaitu:
Jika –ttabel ≤ thitung ≤ +ttabel, maka H0 diterima
10) Bandingkan t-hitung dengan t-tabel
11) Buatlah kesimpulannya
2) Uji atau asumsikan bahwa data berdistribusi normal
3) tentukan apakah variansnya homogen atau hetero?
4) Tulis Ha dan H0 dalam bentuk kalimat
5) Tulis Ha dan H0 dalam bentuk statistik
6) Cari t-hitung atau z-hitung dengan rumus tertentu
7) Tentukan taraf signifikan (α)
8) Cari t-tabel atau z-tabel dengan pengujian dua pihak dimana df yang tergantung rumus.
9) Tentukan kriteria pengujian, yaitu:
Jika –ttabel ≤ thitung ≤ +ttabel, maka H0 diterima
10) Bandingkan t-hitung dengan t-tabel
11) Buatlah kesimpulannya
Pada kesempatan kali ini saya kembali memposting bahasan di bidang statistika, yaitu mengenai uji hipotesis dari 2 rata-rata.
Data dipilih secara acak
Data masing-masing homogen
Uji Beda Rata-rata 2 Sampel
INDEPENDENT SAMPLE 2 TEST (UJI PERBEDAAN 2 SAMPEL INDEPENDEN)
Untuk melakukan uji beda rata-rata dua sampel independen dapat terjadi pada beberapa kondisi. Kondisi pertama adalah dimana nilai varians populasi diketahui sedangkan kondisi kedua dimana nilai varians tidak diketahui.
Berikut merupakan statistik uji yang digunakan dengan kondisi varians populasi diketahui:

Rumus di atas dapat digunakan ketika menuhi asumsi dimana populasi harus berdistribusi normal, observasi sampel dilakukan secara independen, σ1 dan σ2 diketahui.
Kondisi kedua adalah uji beda rata-rata dimana nilai varians populasi tidak diketahui. Statistik uji yang cocok digunakan adalah nilai t statistik dengan formula sebagai berikut:
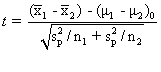
PAIRED SAMPLE 2 TEST (UJI DUA SAMPEL BERPASANGAN)
Perbedaan paired sample dengan independent sample adalah terletak pada kelompok yang kita bandingkan. Jika kelompok yang kita bandingkan berasal dari populasi yang berbeda maka disebut dengan independent sample. sebaliknya jika kelompok yang dibandingkan berasal dari populasi yang sama maka disebut paired sample. Contohnya adalah kita membandingkan tingkat kemiskinan di suatu daerah pada dua periode yang berbeda. Berikut merupakan formula yang dapat digunakan untuk uji beda rata-rata pada paired sample.
(perbedaan mean harus berdistribusi normal) dan
 tidak diketahui or dengan ukuran sampel n < 30.
tidak diketahui or dengan ukuran sampel n < 30.Z=

Contoh Kasus dalam pengerjaan pengujian signifikansi (hipotesis)
Suatu kegiatan penelitian eksperimental, telah berhasil menemukan metode “ABG” sebagai metode baru untuk mengajarkan mata kuliah Statistika II. Dalam rangka uji coba terhadap efektifitas atau keampuhan metode baru itu, dilaksanakan penelitian lanjutan dengan mengajukan Hipotesis Nol (Nihil) yang mengatakan : Tidak terdapat perbedaan yang signifikan nilai Statistika II antara sebelum dan sesudah di terapkannya metode “ABG” sebagai metode mengajar mahasiswa UIB sem 6. Dalam rangka pengujian ini diambil sampel sebanyak 20 mahasiswa. Gunakan taraf kepercayaan 95 % (alfa=5% ) untuk menguji pernyataan (Hipotesis) tersebut.
Datanya Sebagai berikut:
| Nama | Nilai Statistika II | |
| Sebelum | Sesudah | |
| A | 78 | 75 |
| B | 60 | 68 |
| C | 55 | 59 |
| D | 70 | 71 |
| E | 57 | 63 |
| F | 49 | 54 |
| G | 68 | 66 |
| H | 70 | 74 |
| I | 81 | 89 |
| J | 30 | 33 |
| K | 55 | 51 |
| L | 40 | 50 |
| M | 63 | 68 |
| N | 85 | 83 |
| O | 70 | 77 |
| P | 62 | 69 |
| Q | 58 | 73 |
| R | 65 | 65 |
| S | 75 | 76 |
| T | 69 | 86 |
Maka Langkah -langkah yang perlu dilakukan:
- Menentukan Hipotesis yang digunakan, yaitu:

(Tidak terdapat perbedaan yang signifikan antara hasil belajar sebelum dan sesudah)
(Terdapat perbedaan yang signifikan hasil belajar sebelum dan sesudah) - Tetapkan titik kritis yaitu alfa 5%
- Tentukan daerah kritis, dengan db = n -1=20-1=19
- Tentukan t hitung
- Memulai dengan menghitung D(selisih).

- Menghitung Standar Deviasi:

- Menghitung t hitung:
- Memulai dengan menghitung D(selisih).

Metode Biseksi merupakan salah satu metode tertutup untuk
menentukan solusi akar dari persamaanon linier. Metode Bidang Bebas’ atau
lebih spesifik lagi ‘Metode Bidang Paruh’ (Bisection).
Prinsip dari metode ini adalah “pemaruhan”
(nilai rata-rata) dari nilai estimasi akar suatu Persamaan Aljabar Non-Linier
Tunggal
Metode ini pada umumnya memerlukan 2
(dua) buah tebakan untuk harga-harga x-awal (x0 dan
Prinsip
Utama Metode Biseksi Sebagai Berikut:
1) Menggunakan dua buah nilai awal
untuk mengurung salah satu/ lebih akar persamaan non linier.
2) Nilai akarnya diduga melalui
nilai tengah antara dua nilai awal yang ada.
Representasi
grafik dari metode bisection adalah sebagai berikut :
ž Untuk menggunakan metode
bisection, terlebih dahulu ditentukan batas bawah (a) dan batas atas (b).
Kemudian dihitung nilai tengah: Dari nilai x ini perlu dilakukan pengecekan
keberadaan akar. Secara matematik, suatu range terdapat akar persamaan bila
f(a) dan f(b) berlawanan tanda. Setelah diketahui dibagian mana yang terdapat
akar, maka batas bawah dan batas atas di perbaharui sesuai dengan range dari
bagian yang mempunyai akar.
ž Batasan a dan b memberikan harga
bagi fungsi f(x) untuk x = a dan x = b. Langkah selanjutnya adalah memeriksa
apakah f(a) × f(b) < 0.
ž Dengan rumusan c = (a+b)/2,
diperiksa apakah nilai mutlak f(c ) < 0 (batas simpangan kesalahan). Jika
benar, nilai x = c adalah solusi yang dicari. Jika tidak terpenuhi, ditetapkan
batasan baru dengan mengganti nilai b = c
ž apabila f(a)*f(c) = 0;
proses menemukan c baru dilakukan seperti prosedur yang telah dijelaskan.
Contoh
soal :
Hitung √2 . Misalkan f(x) = 2 – x2.
ž Jawab:
Misalkan f(x) = 2 – x2.
Maka: f(1)=1 dan f(2)=2.
Jadi akar terletak antara x1= 1 dan x2= 2.
Titik tengah xn = ((x_1+x_2)/2)
= ( (1+2) / 2 )
= 3/2 = 1,5
f(x_n ) = 2 - (x_n )^2
f(1,5) = 2 - (1,5)^2
=2-2,25
=-0,25
Misalkan f(x) = 2 – x2.
Maka: f(1)=1 dan f(2)=2.
Jadi akar terletak antara x1= 1 dan x2= 2.
Titik tengah xn = ((x_1+x_2)/2)
= ( (1+2) / 2 )
= 3/2 = 1,5
f(x_n ) = 2 - (x_n )^2
f(1,5) = 2 - (1,5)^2
=2-2,25
=-0,25
ž Kesimpulan:
Dengan
menggunakan metode biseksi dengan tolerasi error 0.001 dibutuhkan10 iterasi,
semakin
teliti (kecil toleransi errornya) maka semakin besar jumlah iterasi yang
dibutuhkan.







berikan saya contoh uji pebedaan 2 sampel independen..?
BalasHapusUJI BEDA 2 SAMPEL YANG N1 TDK SAMA DGN N2 JUMLAHNYA, BGM CARANYA? TERMASUK DIDALAMNYA PROSES SPSS NYA. TERIMA KASIH
BalasHapus